Mochikoro
Esempio
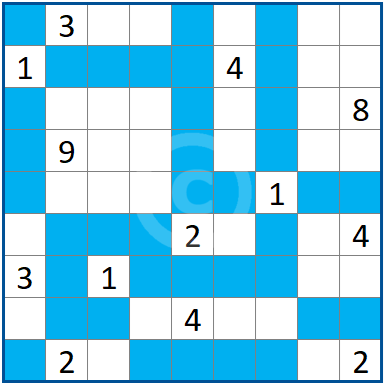
Soluzione
Introduzione
L'obiettivo di questo gioco è quello di suddividere lo schema in aree in modo che alcune di esse siano colorate ed altre rimangano bianche. Le aree bianche, dette isole, devono essere rettangolari o quadrate e non possono essere ortogonalmente adiacenti ad altre isole; ogni isola deve invece essere diagonalmente adiacente ad almeno un'altra isola; tutte le isole devono infine formare un unico gruppo diagonalmente connesso. Ogni casella numerata deve far parte di un'isola, ma alcune aree bianche potrebbero non contenere una casella numerata. Il numero all'interno dell'isola indica da quante caselle è formata l'isola stessa, inclusa la casella numerata. Non possono esserci aree colorate di dimensioni 2x2.
Figura 1
Figura 2
Figura 3
Figura 4
Figura 5
Figura 6
Come si risolve
Proviamo a risolvere lo schema di figura 1.
Cominciamo dalle caselle con il numero 1: queste devono avere tutte le caselle ortogonalmente adiacenti colorate.
Il 3 in alto a sinistra può svilupparsi in un'isola di 3×1 solo verso il basso, poiché espandendosi verso destra si collegherebbe alla casella numerata in c2. Inoltre, le caselle ortogonalmente adiacenti devono essere colorate (vd. figura 2). Per lo stesso motivo, il 3 in b4 può espandersi solo verso destra (vd. figura 3).
Il 4 in c2 non può formare un'area 4×1, ma solo un'area 2×2 tra c2 e d1. Possiamo quindi colorare la casella e2. Per evitare che l'area tra c2 e d1 rimanga isolata, dobbiamo necessariamente collegarla a un'isola 2×1 in e3-f3 (vd. figura 4).
L'isola che comprende il 6 in g6 deve necessariamente svilupparsi in un'area 3×2 tra e5 e g6, altrimenti rimarrebbe isolata dalle altre (vd. figura 5).
Il 3 in c6 deve espandersi verso sinistra, formando un'area 3×1. Per evitare che questa rimanga isolata, deve essere collegata a un'altra isola in d7, che la connetta all'area e6-g5 (vd. figura 6).
Il gioco è risolto!
Ultimo aggiornamento: 28/12/2025



