Epaminondas
Introduzione
Il
gioco è una rielaborazione di Crossings, ideato da Robert Abbott nel
1963. Crossings viene citato nel volume di Sid Sackson A Gamut of
Games del 1969. Nel 1975 il gioco viene pubblicato dallo stesso
autore con il nome di Epaminondas, in onore dell'omonimo stratega
tebano che sconfisse gli Spartani nel 371 A.C. grazie alla
"Falange", particolare formazione da lui stesso ideata.
Nel gioco Crossings il tavoliere è un quadrato 8x8 e le regole di cattura sono differenti rispetto alla successiva rielaborazione.
Come si gioca
Il gioco è composto da:
- un tavoliere quadrato di 168 caselle (14x12);
- 56 pedine (28 bianche e 28 nere).
Le pedine si collocano nelle caselle e non negli incroci.
Si gioca in due.
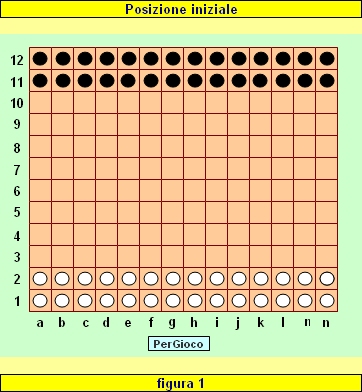
La posizione iniziale è quella riprodotta in figura 1.
Inizia il Bianco.
Le caselle sulla prima traversa (a1, b1, c1, d1, ecc.) costituiscono la "Base" del Bianco, le caselle sull'ultima traversa (a12, b12, c2, d12, ecc.) costituiscono la "Base" del Nero.
Al proprio turno si può effettuare una sola mossa. La mossa è sempre obbligatoria; è infatti vietato "passare".
In questo gioco si possono muovere singole pedine oppure "Falangi".
La Falange è una formazione composta da una fila ininterrotta di due o più pedine del proprio colore, disposte in linea orizzontale, verticale, o diagonale. Una singola pedina può appartenere a più Falangi contemporaneamente. Una Falange (di almeno tre pedine) può essere scomposta in Falangi più piccole. E' possibile muovere una Falange soltanto se esiste almeno una casella libera adiacente ad uno degli estremi. Non è possibile muovere una Falange che abbia entrambi gli estremi bloccati (da pedine di qualsiasi colore).
Esempio:
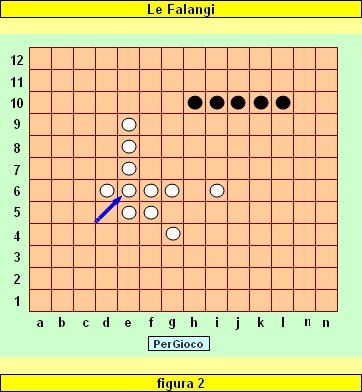
In figura 2 vediamo nella parte superiore del tavoliere una Falange nera composta da cinque pedine. In realtà questa formazione può essere scomposta in Falangi più piccole: il Nero può pertanto muovere la Falange h10-l10 (di cinque pedine), ma anche le Falangi h10-k10 e i10-l10 (entrambe di quattro pedine), h10-j10 e j10-l10 (tre pedine ciascuna), h10-i10 e k10-l10 (due pedine ciascuna). Ognuna di queste Falangi ha almeno una casella libera adiacente ad uno degli estremi.
Il Nero può anche muovere singolarmente una delle cinque pedine h10, i10, j10, k10, o l10.
Sempre in figura 2 vediamo un gruppo di pedine bianche che può essere scomposto nelle seguenti Falangi: e5-e9 (cinque pedine), e6-e9 oppure e5-e8 (quattro pedine), e7-e9 oppure e5-e7 (tre pedine), e8-e9 oppure e5-e6 (due pedine), d6-g6 (quattro pedine), d6-f6 oppure e6-g6 (tre pedine), d6-e6 oppure f6-g6 (due pedine), ed ancora e6-g4 (tre pedine), e6-f5, f5-g4, d6-e5, e5-f5, f5-f6, f5-g6, e7-f6, e5-f6 (due pedine). Ognuna di queste Falangi ha almeno un estremo libero e può pertanto muovere. La pedina in i6 non appartiene ad alcuna Falange. La pedine in e6 (indicata dalla freccia) appartiene a molte delle Falangi sopra citate, ma può anche essere mossa singolarmente.
In figura 2 possono essere individuate ulteriori Falangi, che però non consideriamo, in quanto, non avendo estremi liberi, non possono muovere (come, ad esempio, la Falange nera i10-k10, che ha entrambi gli estremi bloccati).
Le
singole pedine possono essere mosse di una casella per volta in
qualsiasi direzione (orizzontale, verticale o diagonale) sia in
avanti che all'indietro. La casella di arrivo deve essere libera.
Le Falangi si muovono in direzione di uno dei loro estremi (in orizzontale, verticale o diagonale) di un numero di caselle non superiore al numero delle pedine che compongono la Falange stessa. Ad esempio, una Falange composta da quattro pedine, può muovere di una, due, tre o quattro caselle. La casella di arrivo e tutte le caselle transitate dalla Falange devono essere libere. Solo in caso di cattura la Falange può terminare la propria corsa in una casella occupata da una pedina avversaria.
Le Falangi muovono sempre lungo la loro lunghezza, mai lateralmente.
Esempio:
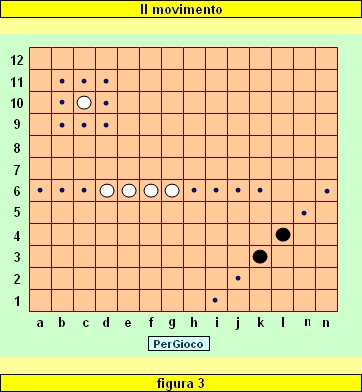
In figura 3 la Falange bianca può muovere solo verso destra (al massimo di quattro caselle) o verso sinistra (in questo caso al massimo di tre caselle, perché un movimento più ampio la porterebbe al di fuori del tavoliere); la Falange nera può muovere verso l'alto oppure verso il basso di un massimo di due caselle.
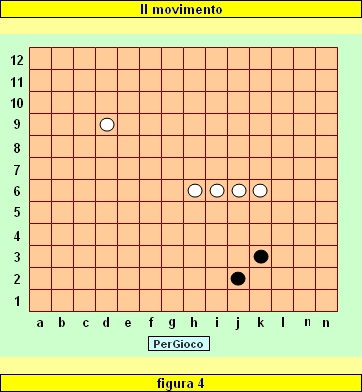
Supponiamo che nella situazione in figura 3 il Bianco muova la pedina c10 in d9, il Nero la Falange k3-l4 in j2 ed infine il Bianco la Falange d6-g6 in k6: la nuova situazione è riprodotta in figura 4.
Alle singole pedine è vietato catturare. La Falange può invece catturare una pedina o una Falange avversaria, andando ad occupare con la propria pedina, posta ad uno degli estremi, una casella occupata da una pedina avversaria. La cattura non è mai obbligatoria; quando sussistono le condizioni per catturare, il giocatore può decidere liberamente se effettuare la presa o meno.
La cattura è possibile quando, al termine di una mossa, uno degli estremi della Falange, si troverebbe su una casella occupata da una pedina avversaria.
Esempio:
In figura 5 la Falange bianca f11-h11 può muovere verso sinistra di una, due o anche di tre caselle. Se muove di tre caselle, termina la sua corsa sulla casella c11, occupata da una pedina avversaria, facente parte di una Falange composta da due pedine. La Falange bianca cattura la Falange avversaria, che viene rimossa dal tavoliere.
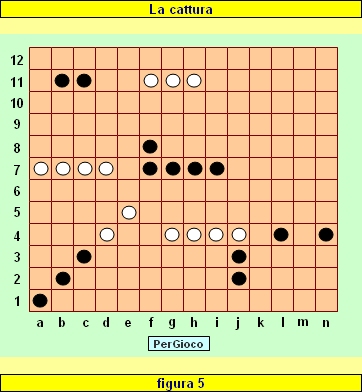
La cattura è possibile quando la Falange catturante è composta da un numero di pedine superiore a quello delle pedine che compongono la Falange catturata (nel caso in cui venga catturata una singola pedina, la Falange che effettua la cattura deve essere composta da almeno due pedine).
Esempio:
In figura 5 le Falangi che si trovano sulla settima traversa (a7-d7 e f7-i7) sono composte entrambe da 4 pedine e pertanto nessuna delle due è in grado di catturare l'altra.
Inoltre la Falange bianca d4-e5 non può catturare la Falange nera a1-c3, in quanto si trova in inferiorità numerica (due pedine contro tre dell'avversario).
In caso di cattura, la Falange catturata deve essere sempre considerata nella sua massima lunghezza, e non può pertanto essere scomposta in Falangi più piccole.
Esempio:
in figura 5 la Falange bianca a7-d7 non può catturare la Falange nera f7-i7, ma nemmeno le Falangi più piccole f7-h7, f7-g7 o la pedina f7.
La
Falange deve terminare la cattura in modo da occupare una sola casella
precedentemente occupata dall'avversario e non può proseguire la sua corsa
oltre la prima pedina avversaria catturata.
Esempio:
in figura 5 la Falange nera a1-c3 può catturare la Falange bianca d4-e5 e termina la sua corsa non oltre la prima casella precedentemente occupata da una pedina avversaria (e cioè in d4). Pertanto, al termine della cattura, la Falange nera occuperà le caselle da b2 a d4.
Allo stesso modo, la Falange bianca g4-j4 può catturare la pedina nera in l4; al termine della cattura occuperà le caselle da i4 a l4.
La pedina catturata viene immediatamente rimossa dal tavoliere. La Falange catturata viene anch'essa completamente rimossa dal tavoliere (non viene catturata soltanto la prima pedina, ma l'intera formazione).
Abbiamo visto che in figura 5 la Falange nera f7-i7 non può essere catturata dall'avversario. Il Bianco potrebbe però utilizzare la Falange d4-e5 per catturare la pedina in g7 e "spezzare" la Falange avversaria in due tronconi. Successivamente la pedina in f7 sarebbe catturabile dal Bianco (ma anche la pedina g7 da parte della Falange nera h7-i7).
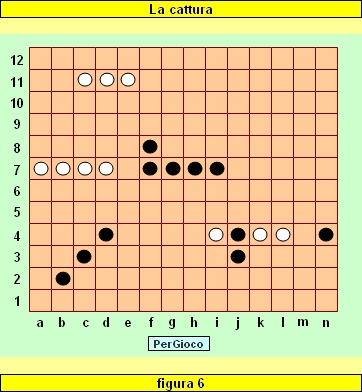
Supponiamo che nella situazione in figura 5 vengano effettuate, nell'ordine, le seguenti catture: f11-h11 in c11, a1-c3 in d4, g4-j4 in l4, j2-j3 in j4. La nuova situazione è riprodotta in figura 6.
Lo scopo del gioco è avere sulla Base opposta alla propria (la traversa 12 per il Bianco e la traversa 1 per il Nero), all'inizio del proprio turno, una pedina in più dell'avversario.
Quando uno dei giocatori raggiunge con una propria pedina la Base opposta alla propria, l'avversario deve immediatamente difendersi per evitare la sconfitta all'inizio del turno successivo, e lo può fare in due modi:
a) catturare la pedina avversaria che si trova sulla propria Base;
b) raggiungere con una propria pedina la Base avversaria, pareggiando i conti.
Se riesce a difendersi in uno dei modi citati, allora la partita prosegue.
Esempio:
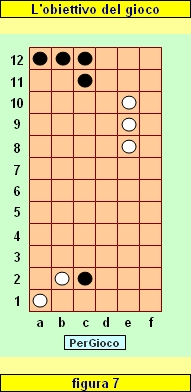
Nella situazione in figura 7 (su un tavoliere ridotto) tocca al Bianco, il quale potrebbe minacciare la vittoria muovendo la Falange e8-e10 verso la Base avversaria.
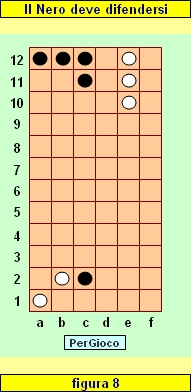
In figura 8 vediamo che dopo la mossa e8-e10->e12 il Bianco ha una pedina (e12) sulla Base avversaria e il Nero non ha invece pedine sull'altra Base (traversa 1). Se permarrà questa situazione dopo l'eventuale difesa del Nero, il Bianco avrà vinto, perché all'inizio del turno successivo avrà una pedina in più sulla Base avversaria.
Ora il Nero può difendersi in
due modi:
a) catturando la pedina e12;
b) raggiungendo con una propria pedina la Base avversaria, muovendo, ad esempio c2->d1.
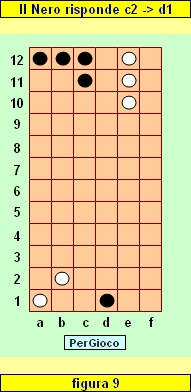
Supponiamo che il Nero scelga la seconda possibilità: ora sia il Bianco che il Nero hanno una pedina sulla Base avversaria e la partita, pertanto, prosegue (vd. figura 9).
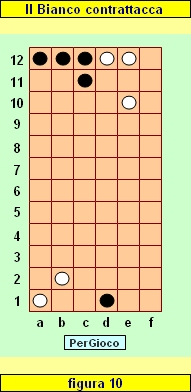
Ora il Bianco contrattacca muovendo la pedina e11 in d12: ora il Bianco ha due pedine sulla Base avversaria (una in più del Nero). Se il Nero non rimedierà entro la mossa successiva, il Bianco avrà vinto la partita (vd. figura 10).
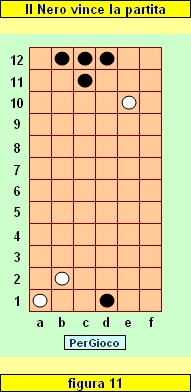
Il Nero risponde catturando la Falange d12-e12 con la propria formazione a12-c12. Ora il Nero ha una pedina sulla Base avversaria; il Bianco non ha pedine sulla Base avversaria e non ha alcuna possibilità di controbattere. Il Nero vince la partita (vd. figura 11).
Varianti
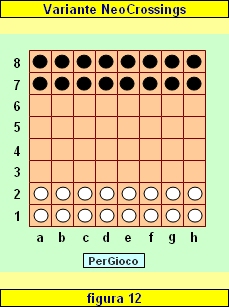
Variante NeoCrossings
Questa variante si gioca con le regole di Epaminondas, ma su un tavoliere di Crossings (8 caselle per lato), e 32 pedine (16 a testa). La posizione iniziale è quella riprodotta in figura 12.
abstractgamesmagazine.com/epaminondas.html
Ultimo
aggiornamento:
08/12/2008
- Per suggerimenti e contributi:
E-mail