Tangram
Introduzione
Il Tangram è un celebre rompicapo cinese composto da sette pezzi geometrici che permettono di creare moltissime figure. Secondo la leggenda, un imperatore aveva ordinato una grande lastra di vetro perfettamente quadrata per il suo palazzo. Durante il trasporto, la lastra cadde e si frantumò in sette pezzi dalle forme regolari. Gli inservienti la presentarono come un rompicapo e l’imperatore, divertito, scoprì che quei frammenti consentivano di formare molte altre figure, trasformando un incidente in un raffinato passatempo di corte.
Oltre alla leggenda, esistono dati storici concreti. Secondo Jerry Slocum, il Tangram si sviluppa in Cina tra il 1796 e il 1801. Già nel 1780 l’artista giapponese Kitagawa Utamaro mostra due donne cinesi che lo usano. La più antica pubblicazione nota risale al 1813 (con ristampe del 1815), con silhouette nere da ricostruire usando tutti i pezzi.
Grazie ai contatti commerciali, il Tangram conquista rapidamente Europa e America. Nel 1817 esplode la moda in Inghilterra con libretti di enigmi e carte illustrate, diffondendosi poi in Francia, Italia, Germania, Olanda, Danimarca, Svezia, Austria, Svizzera, Stati Uniti. Il rompicapo appassiona anche personaggi illustri come Lewis Carroll ed Edgar Allan Poe. In Italia, nel 1817, esce Nuovo e Dilettevole Giuoco Chinese con oltre 300 figure, seguito nel 1818 da Metamorfosi del Giuoco detto l’Enimma Chinese.
Il mito cresce anche grazie all’enigmista americano Sam Loyd, che nel 1903 pubblica The 8th Book of Tan. Secondo la sua fantasia, il gioco risalirebbe a 4000 anni prima, creato dal dio Tan autore di sette libri sacri con mille figure ciascuno. I sette pezzi rappresenterebbero gli astri erranti dell’antichità. Loyd propone 652 figure, tra modelli cinesi e invenzioni originali.
L’origine del nome Tangram resta incerta. Il termine cinese è Ch’i ch’iao t’u, ma varie teorie occidentali lo collegano ai navigatori Tanka, al cantonese Tang (“cinese”) o all’inglese arcaico tangram, “rompicapo”. Nessuna spiegazione è definitiva, ma questo enigma accresce il fascino universale di uno dei più famosi giochi di logica al mondo.
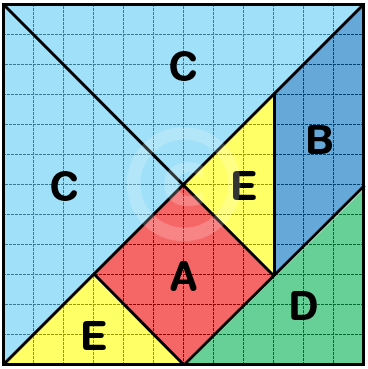
Il Tangram si compone di sette forme geometriche dette tan, ottenute tagliando un quadrato perfetto in:
- un quadrato,
- un parallelogramma,
- due triangoli grandi uguali,
- un triangolo medio,
- due triangoli piccoli.
Il gioco consiste nel formare figure di ogni tipo — animali, persone, oggetti reali o astratti — usando sempre tutti e sette i pezzi, senza sovrapporli, e potendoli ruotare o ribaltare liberamente. Proprio in questa regola semplice si cela la sua ricchezza: da un set fisso di forme nasce un numero praticamente infinito di combinazioni. Si possono creare un cavallo al galoppo, un uomo che corre, una barca a vela o addirittura lettere e numeri.
Relazioni geometriche tra i pezzi
I pezzi del Tangram hanno proporzioni matematiche molto precise:
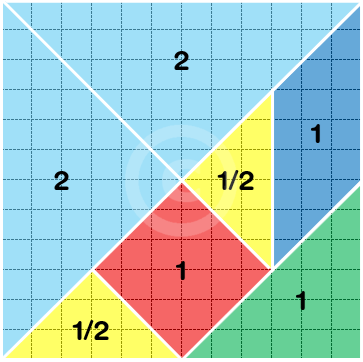
Aree relative:
- ciascun triangolo grande vale 1/4 dell’area totale;
- il triangolo medio, il quadrato e il parallelogramma valgono ciascuno 1/8;
- i due triangoli piccoli hanno 1/16 ciascuno;
- ad esempio, il triangolo grande ha un’area doppia del triangolo medio, e quest’ultimo ha il doppio dell’area di ciascun triangolo piccolo;
- se si assume che l’area del quadrato centrale valga 1, si possono calcolare proporzionalmente tutte le altre.
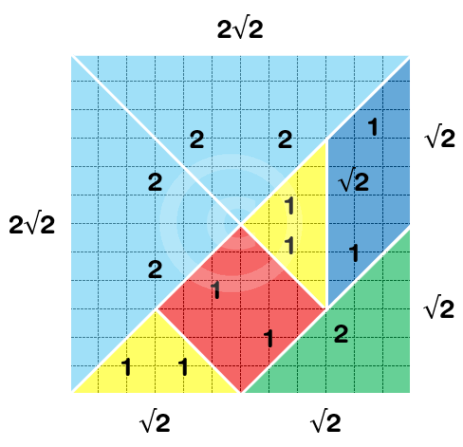
Lati e proporzioni:
- il cateto del triangolo grande coincide con l’ipotenusa del triangolo medio;
- il cateto del triangolo medio coincide con l’ipotenusa del triangolo piccolo e con la diagonale del quadrato;
- il parallelogramma condivide lati con il quadrato e i triangoli piccoli, ma ha forma “obliqua” che permette ribaltamenti e simmetrie particolari;
- se il lato del quadrato di partenza è 1, i lati degli altri tan hanno solo tre lunghezze diverse, basate su multipli di √2.
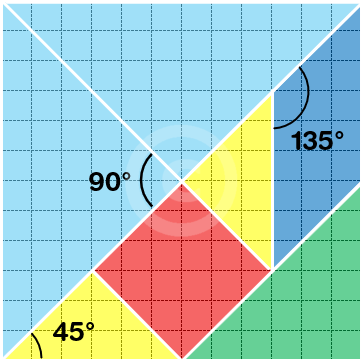
- tutti i triangoli sono rettangoli isosceli, con un angolo di 90° e due di 45°;
- il parallelogramma ha due angoli di 45° e due di 135°;
- complessivamente, nel set ci sono 9 angoli retti, 12 angoli di 45° e 2 angoli di 135°.
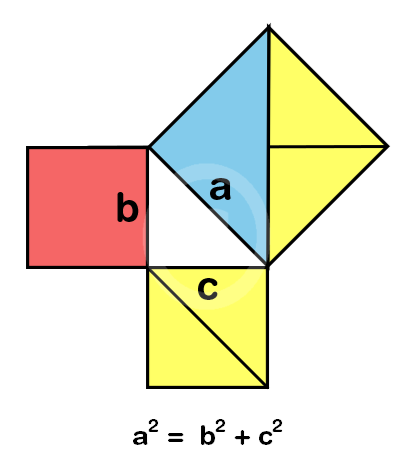
Aspetti matematici e Teorema di Pitagora
Il Tangram è un ottimo strumento per esplorare concetti di area, frazioni, simmetria assiale e centrale, rotazione e traslazione. Tutti i triangoli sono rettangoli isosceli, con cateti uguali e ipotenusa pari a √2 volte il cateto. Il Teorema di Pitagora si applica perfettamente: la somma dei quadrati sui cateti è uguale al quadrato costruito sull’ipotenusa.
Ad esempio, con i pezzi del Tangram è facile verificare che l’area costruita sul cateto del triangolo medio corrisponde alla somma delle aree di due triangoli piccoli. Il parallelogramma, con la sua forma particolare, introduce la possibilità di riflessione e ribaltamento, moltiplicando le varianti di composizione e arricchendo la complessità del gioco.
La scheda del gioco in pdf
Ultimo aggiornamento: 29/11/2025


